One of the biggest, if not the biggest issues of climate science skepticism is the criticism of over-reliance on computer model projections to suggest future outcomes. In this paper, climate models were hindcast tested against actual surface observations, and found to be seriously lacking. Just have a look at Figure 12 (mean temperature -vs- models for the USA) from the paper, shown below:
Fig. 12. Various temperature time series spatially integrated over the USA (mean annual), at annual and 30-year scales. Click image for the complete graph.
…we think that the most important question is not whether GCMs can produce credible estimates of future climate, but whether climate is at all predictable in deterministic terms.
Selected sections of the entire paper, from the Hydrological Sciences Journal is available online here as HTML, and as PDF ~1.3MB are given below:
A comparison of local and aggregated climate model outputs with observed data
Anagnostopoulos, G. G. , Koutsoyiannis, D. , Christofides, A. , Efstratiadis, A. and Mamassis, N. ‘A comparison of local and aggregated climate model outputs with observed data’, Hydrological Sciences Journal, 55:7, 1094 – 1110
Abstract
We compare the output of various climate models to temperature and precipitation observations at 55 points around the globe. We also spatially aggregate model output and observations over the contiguous USA using data from 70 stations, and we perform comparison at several temporal scales, including a climatic (30-year) scale. Besides confirming the findings of a previous assessment study that model projections at point scale are poor, results show that the spatially integrated projections are also poor.
Citation Anagnostopoulos, G. G., Koutsoyiannis, D., Christofides, A., Efstratiadis, A. & Mamassis, N. (2010) A comparison of local and aggregated climate model outputs with observed data. Hydrol. Sci. J. 55(7), 1094-1110.
According to the Intergovernmental Panel on Climate Change (IPCC), global circulation models (GCM) are able to “reproduce features of the past climates and climate changes” (Randall et al., 2007, p. 601). Here we test whether this is indeed the case. We examine how well several model outputs fit measured temperature and rainfall in many stations around the globe. We also integrate measurements and model outputs over a large part of a continent, the contiguous USA (the USA excluding islands and Alaska), and examine the extent to which models can reproduce the past climate there. We will be referring to this as “comparison at a large scale”.
This paper is a continuation and expansion of Koutsoyiannis et al. (2008). The differences are that (a) Koutsoyiannis et al. (2008) had tested only eight points, whereas here we test 55 points for each variable; (b) we examine more variables in addition to mean temperature and precipitation; and (c) we compare at a large scale in addition to point scale. The comparison methodology is presented in the next section.
While the study of Koutsoyiannis et al. (2008) was not challenged by any formal discussion papers, or any other peer-reviewed papers, criticism appeared in science blogs (e.g. Schmidt, 2008). Similar criticism has been received by two reviewers of the first draft of this paper, hereinafter referred to as critics. In both cases, it was only our methodology that was challenged and not our results. Therefore, after presenting the methodology below, we include a section “Justification of the methodology”, in which we discuss all the critical comments, and explain why we disagree and why we think that our methodology is appropriate. Following that, we present the results and offer some concluding remarks.
Here’s the models they tested:
Comparison at a large scale
We collected long time series of temperature and precipitation for 70 stations in the USA (five were also used in the comparison at the point basis). Again the data were downloaded from the web site of the Royal Netherlands Meteorological Institute (http://climexp.knmi.nl). The stations were selected so that they are geographically distributed throughout the contiguous USA. We selected this region because of the good coverage of data series satisfying the criteria discussed above. The stations selected are shown in Fig. 2 and are listed by Anagnostopoulos
(2009, pp. 12-13).
Fig. 2. Stations selected for areal integration and their contribution areas (Thiessen polygons).
In order to produce an areal time series we used the method of Thiessen polygons (also known as Voronoi cells), which assigns weights to each point measurement that are proportional to the area of influence; the weights are the “Thiessen coefficients”. The Thiessen polygons for the selected stations of the USA are shown in Fig. 2.
The annual average temperature of the contiguous USA was initially computed as the weighted average of the mean annual temperature at each station, using the station’s Thiessen coefficient as weight. The weighted average elevation of the stations (computed by multiplying the elevation of each station with the Thiessen coefficient) is Hm = 668.7 m and the average elevation of the contiguous USA (computed as the weighted average of the elevation of each state, using the area of each state as weight) is H = 746.8 m. By plotting the average temperature of each station against elevation and fitting a straight line, we determined a temperature gradient θ = -0.0038°C/m, which implies a correction of the annual average areal temperature θ(H - Hm) = -0.3°C.
The annual average precipitation of the contiguous USA was calculated simply as the weighted sum of the total annual precipitation at each station, using the station’s Thiessen coefficient as weight, without any other correction, since no significant correlation could be determined between elevation and precipitation for the specific time series examined.
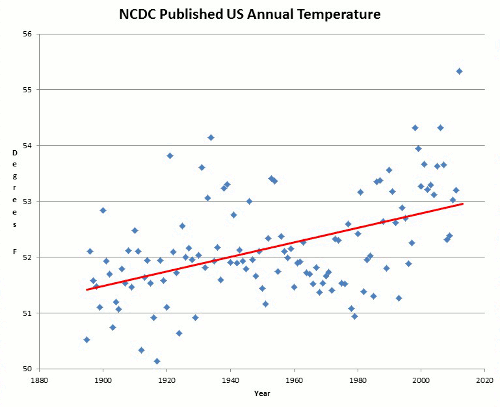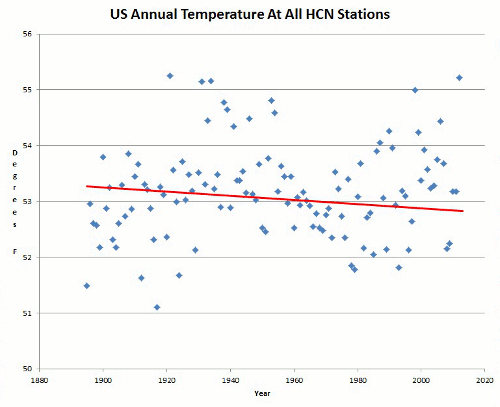
We verified the resulting areal time series using data from other organizations. Two organizations provide areal data for the USA: the National Oceanic and Atmospheric Administration (NOAA) and the National Aeronautics and Space Administration (NASA). Both organizations have modified the original data by making several adjustments and using homogenization methods. The time series of the two organizations have noticeable differences, probably because they used different processing methods. The reason for calculating our own areal time series is that we wanted to avoid any comparisons with modified data. As shown in Fig. 3, the temperature time series we calculated with the method described above are almost identical to the time series of NOAA, whereas in precipitation there is an almost constant difference of 40 mm per year.
Fig. 3. Comparison between areal (over the USA) time series of NOAA (downloaded from http://www.ncdc.noaa.gov/oa/climate/research/cag3/cag3.html) and areal time series derived through the Thiessen method; for (a) mean annual temperature (adjusted for elevation), and (b) annual precipitation.
Determining the areal time series from the climate model outputs is straightforward: we simply computed a weighted average of the time series of the grid points situated within the geographical boundaries of the contiguous USA. The influence area of each grid point is arectangle whose “vertical” (perpendicular to the equator) side is (ϕ2 - ϕ1)/2 and its “horizontal” side is proportional to cosϕ, where ϕ is the latitude of each grid point, and ϕ2 and ϕ1 are the latitudes of the adjacent “horizontal” grid lines. The weights used were thus cosϕ(ϕ2 - ϕ1); where grid latitudes are evenly spaced, the weights are simply cosϕ.
It is claimed that GCMs provide credible quantitative estimates of future climate change, particularly at continental scales and above. Examining the local performance of the models at 55 points, we found that local projections do not correlate well with observed measurements. Furthermore, we found that the correlation at a large spatial scale, i.e. the contiguous USA, is worse than at the local scale.
However, we think that the most important question is not whether GCMs can produce credible estimates of future climate, but whether climate is at all predictable in deterministic terms. Several publications, a typical example being Rial et al. (2004), point out the difficulties that the climate system complexity introduces when we attempt to make predictions. “Complexity” in this context usually refers to the fact that there are many parts comprising the system and many interactions among these parts. This observation is correct, but we take it a step further. We think that it is not merely a matter of high dimensionality, and that it can be misleading to assume that the uncertainty can be reduced if we analyse its “sources” as nonlinearities, feedbacks, thresholds, etc., and attempt to establish causality relationships. Koutsoyiannis (2010) created a toy model with simple, fully-known, deterministic dynamics, and with only two degrees of freedom (i.e. internal state variables or dimensions); but it exhibits extremely uncertain behaviour at all scales, including trends, fluctuations, and other features similar to those displayed by the climate. It does so with a constant external forcing, which means that there is no causality relationship between its state and the forcing. The fact that climate has many orders of magnitude more degrees of freedom certainly perplexes the situation further, but in the end it may be irrelevant; for, in the end, we do not have a predictable system hidden behind many layers of uncertainty which could be removed to some extent, but, rather, we have a system that is uncertain at its heart.
Do we have something better than GCMs when it comes to establishing policies for the future? Our answer is yes: we have stochastic approaches, and what is needed is a paradigm shift. We need to recognize the fact that the uncertainty is intrinsic, and shift our attention from reducing the uncertainty towards quantifying the uncertainty (see also Koutsoyiannis et al., 2009a). Obviously, in such a paradigm shift, stochastic descriptions of hydroclimatic processes should incorporate what is known about the driving physical mechanisms of the processes. Despite a common misconception of stochastics as black-box approaches whose blind use of data disregard the system dynamics, several celebrated examples, including statistical thermophysics and the modelling of turbulence, emphasize the opposite, i.e. the fact that stochastics is an indispensable, advanced and powerful part of physics. Other simpler examples (e.g. Koutsoyiannis, 2010) indicate how known deterministic dynamics can be fully incorporated in a stochastic framework and reconciled with the unavoidable emergence of uncertainty in predictions.















No comments:
Post a Comment